|
Micro-Raman Spectroscopy
IntroductionA brief look at Raman scattering theory. 1. The Raman Effect and Normal Raman Scattering. When light is scattered from a molecule most photons are elastically scattered. The scattered photons have the same energy (frequency) and, therefore, wavelength, as the incident photons. However, a small fraction of light (approximately 1 in 107 photons) is scattered at optical frequencies different from, and usually lower than, the frequency of the incident photons. The process leading to this inelastic scatter is the termed the Raman effect . Raman scattering can occur with a change in vibrational, rotational or electronic energy of a molecule. Chemists are concerned primarily with the vibrational Raman effect. We will use the term Raman effect to mean vibrational Raman effect only. The difference in energy between the incident photon and the Raman scattered photon is equal to the energy of a vibration of the scattering molecule. A plot of intensity of scattered light versus energy difference is a Raman spectrum. 1.1. The Scattering Process. The Raman effect arises when a
photon is incident on a molecule and interacts with the electric dipole
of the molecule. It is a form of electronic (more accurately, vibronic)
spectroscopy, although the spectrum contains vibrational frequencies. In
classical terms, the interaction can be viewed as a perturbation of the
molecule’s electric field. In quantum mechanics the scattering is
described as an excitation to a virtual state lower in energy than a
real electronic transition with nearly coincident de-excitation and a
change in vibrational energy. The scattering event occurs in 10-14
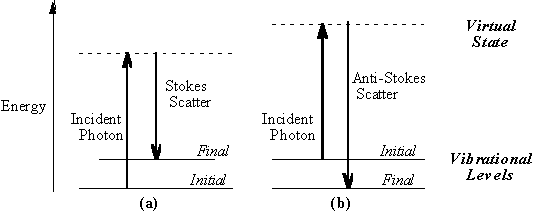
seconds or less. The virtual state description of scattering is shown in
Figure 1.1a.
The energy difference between the
incident and scattered photons is represented by the arrows of different
lengths in Figure 1.1a. Numerically, the energy difference between the
initial and final vibrational levels,
in which l incident and l scattered are the wavelengths (in cm, in MCPF, Ar+ laser wavelength is 5.14E-5 cm, He-Ne is 6.33E-5cm) of the incident and Raman scattered photons, respectively. The vibrational energy is ultimately dissipated as heat. Because of the low intensity of Raman scattering, the heat dissipation does not cause a measurable temperature rise in a material. At room temperature the thermal population of vibrational excited states is low, although not zero. Therefore, the initial state is the ground state, and the scattered photon will have lower energy (longer wavelength) than the exciting photon. This Stokes shifted scatter is what is usually observed in Raman spectroscopy. Figure 1.1a depicts Raman Stokes scattering. A small fraction of the molecules are in vibrationally excited states. Raman scattering from vibrationally excited molecules leaves the molecule in the ground state. The scattered photon appears at higher energy, as shown in Figure 1.1b. This anti-Stokes-shifted Raman spectrum is always weaker than the Stokes-shifted spectrum, but at room temperature it is strong enough to be useful for vibrational frequencies less than about 1500 cm-1. The Stokes and anti-Stokes spectra contain the same frequency information. The ratio of anti-Stokes to Stokes intensity at any vibrational frequency is a measure of temperature. Anti-Stokes Raman scattering is used for contactless thermometry. The anti-Stokes spectrum is also used when the Stokes spectrum is not directly observable, for example because of poor detector response or spectrograph efficiency. 1.2. Vibrational Energies. The energy of a vibrational mode depends on molecular structure and environment. Atomic mass, bond order, molecular substituents, molecular geometry and hydrogen bonding all effect the vibrational force constant which, in turn dictates the vibrational energy. For example, the stretching frequency of a phosphorus-phosphorus bond ranges from 460 to 610 to 775 cm-1 for the single, double and triple bonded moieties, respectively. Much effort has been devoted to estimation or measurement of force constants. For small molecules, and even for some extended structures such as peptides, reasonably accurate calculations of vibrational frequencies are possible with commercially available software. Vibrational Raman spectroscopy is not limited to intramolecular vibrations. Crystal lattice vibrations and other motions of extended solids are Raman-active. Their spectra are important in such fields as polymers and semiconductors. In the gas phase, rotational structure is resolvable on vibrational transitions. The resulting vibration/rotation spectra are widely used to study combustion and gas phase reactions generally. Vibrational Raman spectroscopy in this broad sense is an extraordinarily versatile probe into a wide range of phenomena ranging across disciplines from physical biochemistry to materials science. 1.3. Raman Selection Rules and Intensities. A simple classical electromagnetic field description of Raman spectroscopy can be used to explain many of the important features of Raman band intensities. The dipole moment, P, induced in a molecule by an external electric field, E, is proportional to the field as shown in equation 2.
The proportionality constant a is the polarizability of the molecule. The polarizability measures the ease with which the electron cloud around a molecule can be distorted. The induced dipole emits or scatters light at the optical frequency of the incident light wave. Raman scattering occurs because a
molecular vibration can change the polarizability. The change is
described by the polarizability derivative,
The Raman selection rule is analogous to the more familiar selection rule for an infrared-active vibration, which states that there must be a net change in permanent dipole moment during the vibration. From group theory it is straightforward to show that if a molecule has a center of symmetry, vibrations which are Raman-active will be silent in the infrared, and vice versa. Scattering intensity is
proportional to the square of the induced dipole moment, that is to the
square of the polarizability derivative, If a vibration does not greatly change the polarizability, then the polarizability derivative will be near zero, and the intensity of the Raman band will be low. The vibrations of a highly polar moiety, such as the O-H bond, are usually weak. An external electric field can not induce a large change in the dipole moment and stretching or bending the bond does not change this. Typical strong Raman scatterers are moieties with distributed electron clouds, such as carbon-carbon double bonds. The pi-electron cloud of the double bond is easily distorted in an external electric field. Bending or stretching the bond changes the distribution of electron density substantially, and causes a large change in induced dipole moment. Chemists generally prefer a quantum-mechanical approach to Raman scattering theory, which relates scattering frequencies and intensities to vibrational and electronic energy states of the molecule. The standard perturbation theory treatment assumes that the frequency of the incident light is low compared to the frequency of the first electronic excited state. The small changes in the ground state wave function are described in terms of the sum of all possible excited vibronic states of the molecule. 1.4. Polarization Effects. Raman scatter is partially polarized, even for molecules in a gas or liquid, where the individual molecules are randomly oriented. The effect is most easily seen with an exciting source which is plane polarized. In isotropic media polarization arises because the induced electric dipole has components which vary spatially with respect to the coordinates of the molecule. Raman scatter from totally symmetric vibrations will be strongly polarized parallel to the plane of polarization of the incident light. The scattered intensity from non-totally symmetric vibrations is 3/4 as strong in the plane perpendicular to the plane of polarization of the incident light as in the plane parallel to it. The situation is more complicated in a crystalline material. In that case the orientation the crystal is fixed in the optical system. The polarization components depend on the orientation of the crystal axes with respect to the plane of polarization of the input light, as well as on the relative polarization of the input and the observing polarizer. Go Top 2. Comparison of IR and
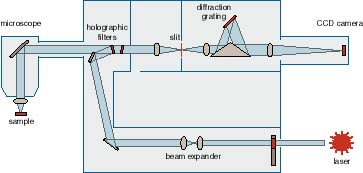
Raman. Go Top InstrumentOptical Characterisation lab equipped with Renishaw RM 3000 Micro-Raman system. Its specification as below:
Operating principles
Go Top Sample PreparationThe great advantage Raman has over infrared spectroscopy is that
the sample can be contained or sealed in a glass (Pyrex) tube because
Raman scattered light in the visible region is not absorbed by glass.
Thus Raman spectra of hygroscopic, corrosive, or oxygen-sensitive
compounds can be measured by sealing them in glass tubing or bottles. It
should be noted, however, that some glass tubing gives rise to
fluorescence or spikes if contaminated with rare earth salts. Raman
spectra of aqueous solutions can be measured easily because water is a
very weak Raman scatterer. Gases Normally the sample gas is contained in glass tubing of diameter 1~2cm and thickness ~1mm. If necessary, the gas may be sealed in small capillary tubing
whose diameter is slightly larger than that of the laser beam. Liquids Liquid samples may be sealed in ampoules, tubing, or capillaries,
depending on the amount of the sample available. For micro quantities (~10-9 liter), capillaries as small as 0.5— 0.1 mm bore
and ~1 mm in length can be used. If
the solution contains particulate matter, strong spike noise may appear
in the spectrum.
Solids Most of the solid samples can be directly
measured with our Micro-Raman. The beam size is 5-20 micron (50-10X
objective), so as small as 50-100 micron area can be analyzed. Powdered samples also can be directly analyzed. Tiny amount may be
packed in ampoules or capillaries, and their Raman spectra are measured
in exactly the same manner as liquid samples. If the sample is colored, efficient absorption of the laser radiation may occur, causing local heating and sometimes sample decomposition. To minimize this problem, we can dilute the sample concentration in a pellet (with KBr) or in solution, and using the defocused laser beam. Go Top ResourceRenishaw Homepage http://www.renishaw.com Go Top Last updated on 20/01/2005 |
||||||||||||||||||||||||||||||||||||